RLHF and PPO – Ferina

给定同一个输入，模型生成的多个候选回答中，人类会对这些回答进行排序。RM 需要学会预测这个排序。

1. 数据格式

假设对于同一个 prompt，我们有两段候选回答：

chosen (c) → 人类更喜欢的回答
rejected (r) → 人类不喜欢的回答

Reward Model 会给它们各自输出一个分数：

[
R_\theta(x, y_c), \quad R_\theta(x, y_r)
]

其中：

(x) 是输入（prompt），
(y_c, y_r) 是回答，
(R_\theta) 是 RM 的打分函数。

2. 目标

我们希望 RM 的分数满足：

[
R_\theta(x, y_c) > R_\theta(x, y_r)
]

3. 损失函数（Reward Model loss）

常用的是 pairwise ranking loss（成对排序损失），公式是：

[
L(\theta) = – \mathbb{E}{(x, y_c, y_r)} \Big[ \log \sigma\big( R\theta(x, y_c) – R_\theta(x, y_r) \big) \Big]
]

其中：

(\sigma(z) = \frac{1}{1 + e^{-z}}) 是 sigmoid 函数，
直观理解：RM 学会把 “chosen” 的分数推高，“rejected” 的分数压低。

4. 简单解释

如果 (R_\theta(y_c) \gg R_\theta(y_r))，说明 RM 判断正确，loss 会很小。
如果 (R_\theta(y_c) \approx R_\theta(y_r))，loss 会比较大，因为模型没有区分开两者。
如果 (R_\theta(y_c) < R_\theta(y_r))，loss 最大，说明模型完全判断错了。

轨迹概率公式

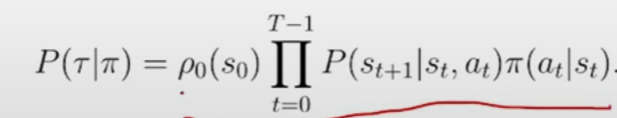
对于一个轨迹在某个策略下的可能性，分析它的影响因素：

初始环境：ρ0（s0）
策略选择概率：Π(at|st)，即在某状态下，该策略选择行动at的概率
环境影响因素：P(st+1|st,at)，有的时候事情并不都如我们所料，因为现实环境具有复杂的特征。在一个下棋的游戏中，我们可以认为这一项恒为1，因为这是一个很确定的场景。但假如，我们是在讨论一个现实场景中的机器人，它不一定会根据选择的策略做出响应的行动，可能关节磨损，可能断电了等等。这一项的核心，在于环境因素会影响agent的状态转移，然后我们把这个转移的概率引入轨迹的计算公式中。

对应的discount reward（折扣回报）

为了防止奖励的发散，同时鼓励更短的path，为奖励的累加添加了根据步数的折扣因子

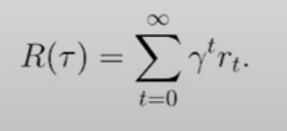
语言模型中的trajectories：从这张图中能很显然的看出来state和action。state指每次都会把当前得到的prompt输进去，action指根据这个prompt选择一个token，然后重复这个过程

梯度优化策略的公式推导过程：

1. 期望展开
2. 梯度符号移动
3. 一个对数的小策略：把概率提取出来
4. 把提取出来的概率转化回期望的形式
5. 代入轨迹概率公式，发现除了策略选择概率之外，初始环境和中间的环境影响和 θ 无关被消掉
补充：这里的 θ 就是参数，通常是神经网络权重和偏置。根据常识，我们的神经网络回根据这些参数，将input转化为一个确定的output，也因此，这个参数实际上决定了策略选择概率

当然，我们在计算这样的期望的时候，不可能真的计算所有轨迹的情况。因此在这里，采用的是样本估计的方法。这时候我们很容易就能把它和所谓的“训练数据”联系起来，也能理解为什么数据有质量的差别，因为本质上，他们都是用来逼近理想期望的。

因此，我们能得到如上图的强化学习基本流程

1. 定义网络和策略
2. 用策略在网络上跑，得到一些轨迹对应的reward
3. 用这些样本去计算梯度
4. 用随机梯度上升法，更新网络里面的参数
5. 回到第二步

所谓的强化，从这个流程上来讲，就是一个这样迭代的过程，目的是使J(Πθ )最大化，也即优化策略使agent在进行action的时候，尽可能获得更多的reward

对于语言模型的强化学习流程：

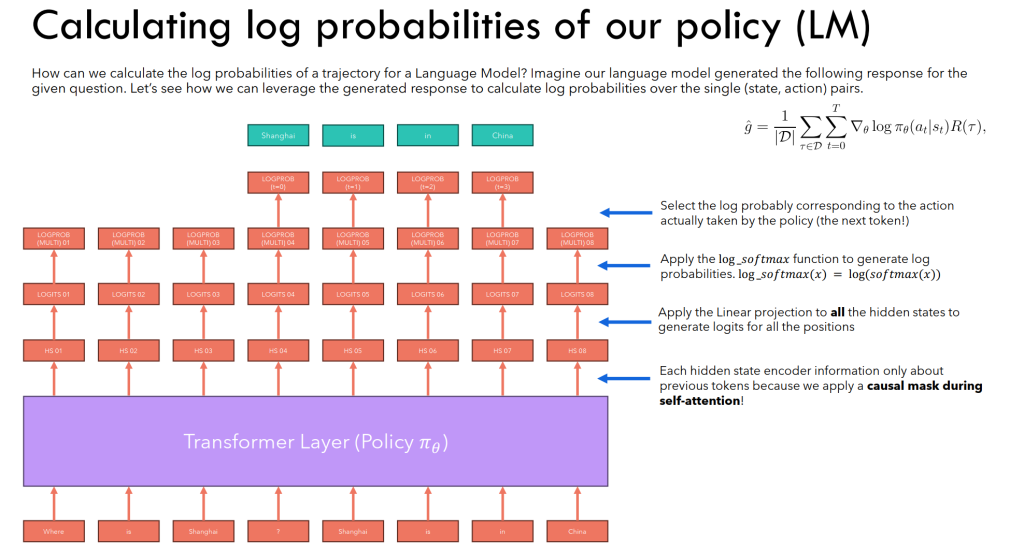
logits 是一个长度为词表大小的向量，每个分量是“候选下一个 token 的未归一化分数”。
把 logits 经过 softmax → 概率分布，再通过 贪心/采样/温度/Top-k/Top-p 等策略，就能最终决定下一个 token。
在上图中的一个实例中，我们可以看出，在经过transformer处理之后，每一个token处都对应生成了一个logits，对应了当输入了这个token及之前的所有token时，model对下一个token的判断
根据轨迹的知识，很容易这样得到每个位置对应的概率选择分数。比如在“？”这个state下，进行action“Shanghai”的概率，其实就是这个位置的logits归一化之后，向量对应“Shanghai”位置的数值。
这个值就可以这样被记录下来，作为后续计算的依据
一个需要注意的事：本质上这个input是由question和answer拼接起来的，而我们其实只需要anwer的那部分。因此question可以被视作是开始的环境，而选择“Shanghai”，才是第一个action。实际上我们需要计算的也只有四步。

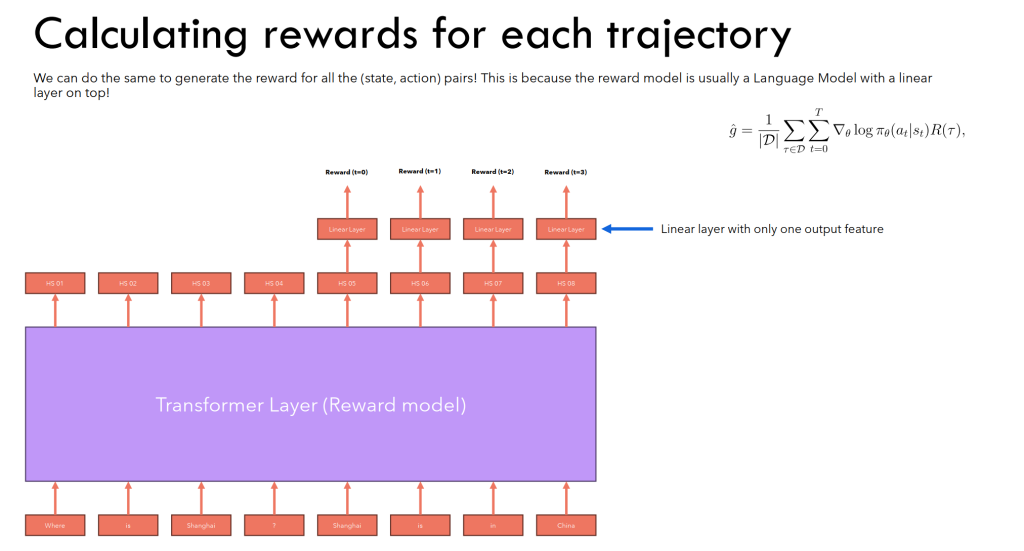
对于Reward计算，类似的可以这样进行，对每一个需要计算reward的地方，过一个线性层输出分数。（回忆之前的discount reward，这里实际上也要这么计算，因为本质上生成一个token类似于cat走一步，所以在计算reward时，实际上是一个累加）
纠正一个思维误区：我之前好像认为对于项，R（r）这个值是在这一步之前所有的奖励分量累加，但这实际上是一个错误，因为在公式推导的过程中，并没有任何一步表示了这个意思，从头到尾这一项都代表了对于整条轨迹来说的奖励项之和，也就是对于一条轨迹来说，这一项是定值，只不过在计算的时候需要考虑在每一步中的奖励分量。

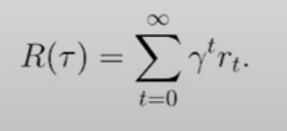
补充一个训练上的疑惑：之前一直在想，如果这样输入的话，那”比较“这个概念就不知道怎样体现了。实际上，真正训练时候，是以batch为单位，每一个batch对应一个Q和若干A，A带有人为的标注。这样的一个batch才是一个有效的训练数据，可以进行训练。

更好的奖励函数：Reward-to-go

之前提到，在计算每一项的时候，奖励项是一个定值。但从常识的角度上来讲，未来的动作不会影响过去的奖励，也因此，对于比较后面的动作来说，由于它实际上根本不会改变前面的奖励项，这些项对这里的梯度是没有贡献的。相当于噪声。
因此将原本的全轨迹回报改为reward-to-go，只计算这之后的奖励项的影响
全轨迹回报：R(τ)=1+2+3=6
reward-to-go：
G0=1+2+3=6
G1=2+3=5
G2=3
Reward-to-go 的核心原理是 因果性：当前动作只影响未来奖励
公式成立的原因：对于 t 时刻之前的奖励，它对 ∇θlog⁡πθ(at∣st)\nabla_\theta \log \pi_\theta(a_t|s_t)∇θlogπθ(at∣st) 的期望为 0
好处：降低梯度方差，使策略梯度更稳定

另一种方式：baseline

在奖励项中引入一个baseline，可以是常数，也可以是和s和Π有关的一个函数，称为Value函数

VΠ(s)，在这里的意义和“未来的期望奖励”有关，表示在当前策略和状态下，对未来能得到奖励的预期
和Reward类似的，这个函数也可以用那种模式来预测

引入这两项后，得到了最后的形态：Aπ(s,a) —Advantage function

优势函数 Aπ(s,a)A^\pi(s,a)Aπ(s,a) 描述的是 在状态 s 下，采取动作 a 相对于平均水平的好坏： Aπ(s,a)=Qπ(s,a)−Vπ(s)

Qπ(s,a)：策略 π 下，从状态 s 采取动作 a 的期望累积回报
Vπ(s)：策略 π 下，从状态 s 开始的平均期望回报（即采取动作的平均水平）

直观解释：

Advantage function 衡量某个 action 在当前状态下，比“平均动作”多赚了多少奖励。

A(s,a)>0：这个动作比平均水平好

A(s,a)<0：这个动作比平均水平差

A(s,a)=0：动作与平均水平一样好

而本质上我们要做的梯度上升的过程，就是让更好的动作，更可能发生。

PS：这个减去平均水平的比方真的很形象，一下感觉回到了高中数学，做统计表的时候

解决计算问题：怎样计算Aπ(s,a)

上面这些计算体现出一些问题
第一种方式：使用了一个平均值代替了后面所有的具体行动值，high bias
随着展开的越来越多，bias降低了，但是方差variance提高了
这是一个在两者之间平衡的问题
因此最后，通过下面这个递归的方式计算Aπ(s,a)

1 Off-Policy Learning（离策略学习）

定义：使用 行为策略 (\mu(a|s)) 生成数据，但训练/优化的是 目标策略 (\pi_\theta(a|s))
优点：
- 可以复用历史数据、旧模型数据、人类演示
- 提高训练效率，不必每次都用最新策略生成
问题：直接使用 (\mu) 的数据更新 (\pi_\theta) 会有偏差 → 需要修正

2 Importance Sampling（重要性采样）

目的：在分布不一致时做期望估计
核心公式：
[
\mathbb{E}{a\sim \pi}[f(a)] = \mathbb{E}{a\sim \mu} \Big[ \frac{\pi(a|s)}{\mu(a|s)} f(a) \Big]
]
含义：用权重 (\frac{\pi}{\mu}) 调整旧数据，使梯度更新无偏
注意事项：
- 权重过大 → 梯度方差大
- 实践中常用 截断 / Clipped IS 降低方差

3 PPO Loss（Proximal Policy Optimization）

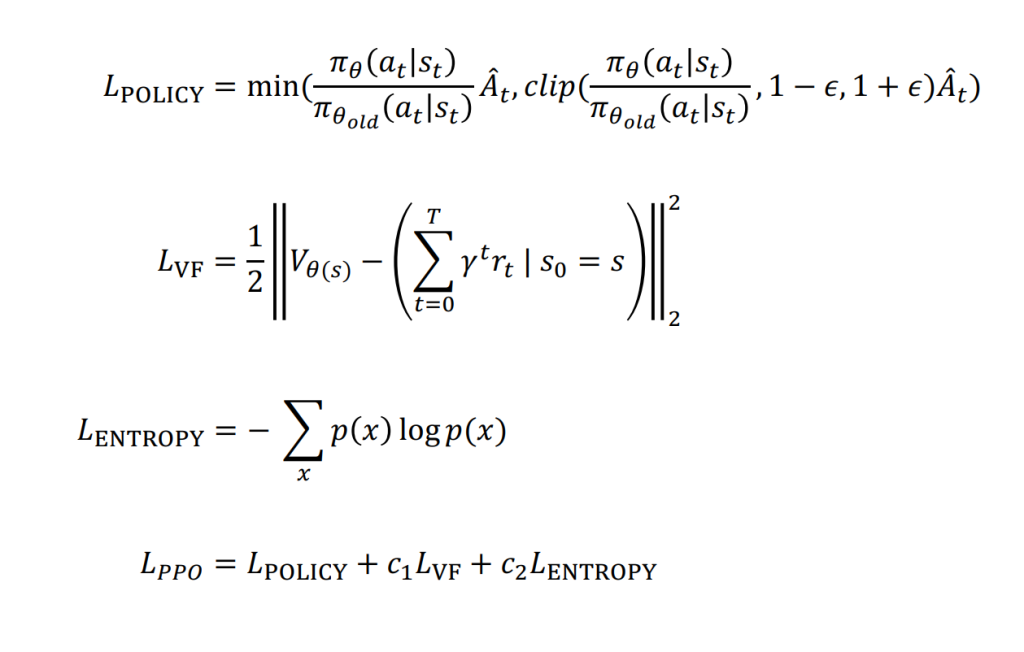
3.1 Clipped Surrogate Loss

[
L^{CLIP}(\theta) = \mathbb{E}_t \Big[ \min \big( r_t(\theta) A_t, \ \text{clip}(r_t(\theta), 1-\epsilon,1+\epsilon) A_t \big) \Big]
]

(r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_\text{old}}(a_t|s_t)}) → 重要性采样比率
(A_t = G_t – V(s_t)) → Advantage function
clip/min → 限制策略更新幅度，保证稳定性

3.2 Value Loss（状态价值损失）

[
L^{VF}(\phi) = (V_\phi(s_t) – G_t)^2
]

用于辅助 Advantage 估计，降低方差

3.3 Entropy Bonus

[
L^S = -\beta H[\pi_\theta(\cdot|s_t)]
]

保持策略探索，防止过早收敛

3.4 总 Loss

[
L^{PPO} = L^{CLIP} – c_1 L^{VF} + c_2 L^S
]

核心思想：
- 利用旧策略数据更新新策略（off-policy + IS）
- 用 Advantage 指导动作选择
- Clip 保证梯度稳定，Entropy 保持探索

Reward Hacking

刚刚提到的所有策略都是为了让model生成更令人满意的结果，但是这些结果不一定是make sense的。比如如果我想让一个model更加的polite，然后把它训成了只会thank you的model，这显然是不好的

因此，我们希望最终生成的模型，不会与原本的模型发生较大的偏移，以此来保证make sense

我们的做法是，保存一个frozen model，当使用Reward model去评判一些token的时候，在奖励函数上减去一个term，代表frozen model和current model对于同样的一个hidden states生成的probability差异。

通过这样的方式，来惩罚对于原始model过大的偏移。

Code

阶段1：数据准备与前向传播

1. `_step_safety_checker` – 输入安全检查 – line 647

输入：

queries: List[torch.LongTensor] – 提示文本的token IDs
responses: List[torch.LongTensor] – 旧模型生成响应的token IDs
scores: List[torch.FloatTensor] – 每个response对应的奖励分数
response_masks: Optional – 响应token的掩码

输出： 经过验证和格式化的相同结构数据
作用： 确保输入数据格式正确，避免运行时错误

2. `prepare_model_inputs` – 构建模型输入 – line 691

输入： queries, responses
输出： Dict包含：

input_ids: (batch_size, seq_len) – 拼接后的query+response
attention_mask: (batch_size, seq_len) – padding掩码
作用： 将query和response拼接成统一的模型输入格式

!!! 3. `batched_forward_pass` – 策略模型前向传播 – line 730 核心函数：用于计算log概率和价格函数估计，参考基础知识，这些是计算梯度的重要参数部分

输入： self.model, queries, responses, model_inputs
输出：

all_logprobs: (Batch_Size, Seq_Len-1) – 每个token的log概率
logits_or_none: logits或None
values: (Batch_Size, Seq_Len-1) – 价值函数估计
masks: (Batch_Size, Seq_Len-1) – 有效token掩码
作用： 计算当前策略下各token的概率分布和价值估计

4. `batched_forward_pass` – 参考模型前向传播 – line 741

输入： self.ref_model, queries, responses, model_inputs
输出： 同上，但基于参考模型
作用： 计算参考策略的log概率，用于KL散度计算

!!! 5. `compute_rewards` – 奖励计算 – line 758 定义在 line 1139

输入： scores, all_logprobs, ref_logprobs, masks

scores：是从数据集中得到的原始数据的评分，成为reward需要加上KL散度

输出：

rewards: (Batch_Size, Seq_Len-1) – 每个token的奖励
non_score_reward: 非分数奖励部分
kls: KL散度值
作用： 结合奖励分数和KL惩罚计算每个token的最终奖励

!!! 6. `compute_advantages` – 优势函数计算 line 772 定义在line 1196

这一步的根据是之前提到的递推公式

输入： values, rewards, masks
输出：

values: 价值估计
advantages: (Batch_Size, Seq_Len-1) – 优势函数
returns: (Batch_Size, Seq_Len-1) – 实际上是A + V = Q，是用来做估计用的
作用： 使用GAE(广义优势估计)计算优势函数

阶段2：PPO优化

7. Mini-batch训练循环

在整个batch上执行多轮(ppo_epochs)优化：

外层循环： 随机打乱样本顺序
中层循环： 按backward_batch_size分块
内层循环： 按mini_batch_size进一步分块

8. `batched_forward_pass` – 在线模型前向传播 line 828

输入： 当前模型参数 + mini-batch数据
输出： 当前策略的logprobs, logits, vpreds（这个就是value）
作用： 获取当前策略的输出用于损失计算

9. `train_minibatch` – 核心优化步骤 line 837

输入：

旧策略的logprobs, values
新策略的logprobs, logits, vpreds
advantages, returns, masks

输出： 训练统计信息dict
作用： 计算PPO损失并执行梯度更新

！！！核心函数PPO Loss计算 定义在 line 1224

参考PPO Loss的定义，进行计算

阶段3：统计记录与更新

10. `record_step_stats` – 记录训练统计

输入： 所有前向传播和训练过程的输出
输出： 汇总的训练统计信息
作用： 记录KL散度、奖励、比率等关键指标

11. `kl_ctl.update` – KL控制器更新

输入： 当前KL散度值, batch_size
输出： 更新KL惩罚系数
作用： 自适应调整KL惩罚强度

准备阶段：验证输入 → 构建模型输入
评估阶段：策略模型前向 → 参考模型前向 → 奖励计算 → 优势估计
优化阶段：多轮mini-batch训练 → 损失计算 → 参数更新
记录阶段：统计收集 → KL控制更新 → 学习率调整